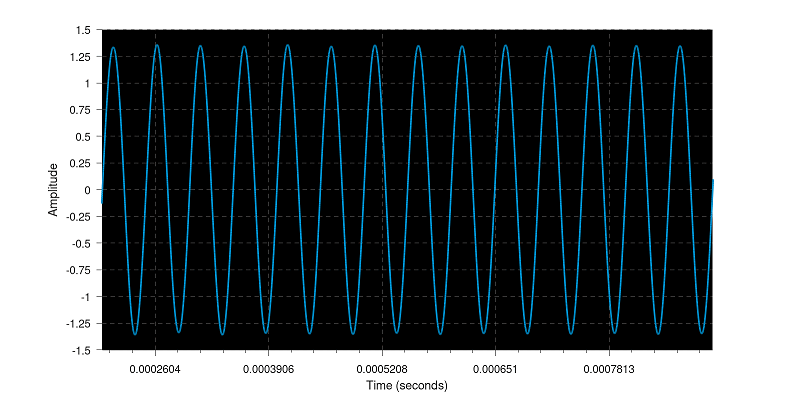
Spoon's Audio Guide: Bit Depth Bit depth determines the dynamic range and the resolution of sound amplitude (volume). To understand bit depth, first visualize how sound is stored, sound is a continuous analog wave, to digitize, snapshots of that wave thousands of times per second (Sample Rate) and measurements of the height of the wave at each snapshot stored at a certain resolution (Bit Depth), here is an example sine wave: Along the wave are measurements, equality spaced horizontally (the sample rate), the vertical height of the measurement is the amplitude, based around a zero line in the middle. Bit Depth therefore determines the resolution (coarseness) of the measurement.

Common Bit Depth Resolutions Everyday bit depths one might come across are:     8-bit: 256 levels (early computers).     16-bit: 65,536 levels (CD quality).     24-bit: 16,777,216 levels (Hi-definition). In addition to these are studio bit depths:     32-bit: 4,294,967,296 levels.     32-bit-float: 24 bit precision (23 bit mantissa), 8 bit exponent, 1 bit sign (6-9 decimal precision).     64-bit-float: 53 bit precision (52 bit mantissa), 11 bit exponent, 1 bit sign (15-17 decimal precision). Why not sell music in best and highest precision? well your playback chain likely has a 16 or 24 bit DAC with better sound cards / devices, even if one had an expensive 32 bit sound card, there is a diminishing return on those extra bits as far as being able to perceive it audibly. Take this crude representation of bit depth as an example: The left speaker could be 8 bit, centre 16 bit and right 24 bit. 8 bit does not have the fidelity of 16 bit and would translate into audible distortion. The difference between 8 bit and 16 bit can be heard with reasonable equipment, however only with the right type of music, modern compressed tracks do nothing for audio quality. Compression squanders the dynamic range, in the name of getting more purchases off radio playback (the louder it sounds more buy). You will see later 8 bit does not have the dynamic range of 16 bit, as long as the audio is mastered to make use of it. Moving onto 16 bit vs 24 bit, if 8 vs 16 was a struggle depending on music, then it is not looking good for 16 vs 24 bit (law of diminishing returns). A blind listening test confirmed as much: the difference between 16 and 24 bit is not distinguishable for most people. Why is there a need then for the other more accurate formats? as already mentioned they are used primarily in the studio, having extra precision allows the track to be processed in a way which is not detrimental to the sound. Floating point also does not suffer from a hard clip limit (more on that later).

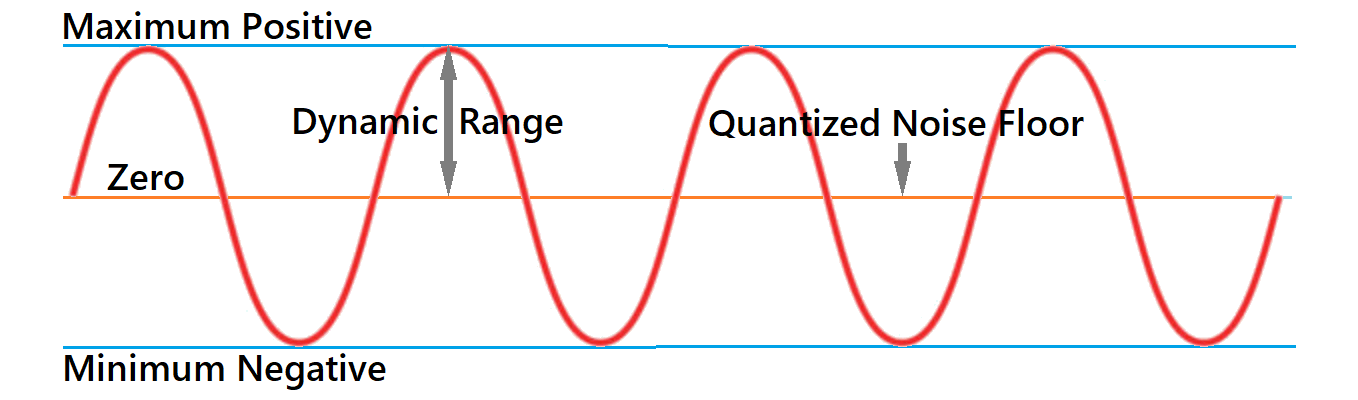
Dynamic Range & Noise Floor Dynamic Range is the distance (in decibels) between the quietest sound effectively captured (the noise floor) and the loudest sound possible before distortion (0 dBFS). In this instance the noise floor is not to be confused with background recording noise, such as humming from a mic, we are talking about the lowest practical signal which can be stored: Each bit depth has different levels a signal can be stored: from the maximum possible value (0 dBFS), to the quietest, notice how the words 'minimum value' was not mentioned, that is because the minimum value is the bottom of full volume sine wave, full minus. In audio the quietest is the zero value, silence, the next one up is the noise floor, in an around zero balanced wave. For every 1 bit of data, you get roughly 6 dB of dynamic range:     8-bit: 8 x 6 = 48 dB of dynamic range.     16-bit: 16 x 6 = 96 dB of dynamic range.     24-bit: 24 x 6 = 144 dB of dynamic range.     32-bit: 32 x 6 = 192 dB of dynamic range.     32-bit-float: (see below).     64-bit-float: 53 x 6 = 318 dB dynamic range (without exponent). When it comes to floating point, it is not as straight forward, floating point has an two components mantissa & exponent. Take 32 bit (non-float) the maximum number that can be stored is +-2 billion, 32 bit floating point though has a maximum value of 34028234663852885981170418348451692544​0, insanely large. Floating point is normally represented in audio in a +-1.0 range, with no exponent. Consider it a ruler, it has 24 bits of precision which can be moved up or down (decimal point is moved) with the exponent. Precision drops though the further one goes from +-1.0, consider the exponent as a multiplier and divider. Yet the exponent is never taken into account when calculating noise floor, yes using one tick of the exponent down reduces precision, however it is still another representation of a number. A discussion Hydrogen Audio : Quantised 32 bit float precision. We will see how that matures, for now are certain that 32 bit float has a noise floor closer between 24 and 32 bit fixed. One can see for floating point the dynamic range is stupidly large, if looking at beyond +1.0 signal, in practical terms +1.0 is the upper limit (see clipping later how float allows this limit to be passed without penalty) so dynamic range is from +-1.0 down to the minimum stored.

Dither Maths can have hidden surprises, one of those is audio dither, the basic premise: adding random low levels of noise when reducing bit depth (for example 64 bit float to 16 bit), can lower the noise floor and increase dynamic range! Adding noise sounds counter-intuitive, why would the signal be intentionally made noisy? well maths again, this noise can be placed in an area which is in-audible, upper frequencies which are above the hearing range (Sample Rate primer).

How Dither Works When lowering bit depth of audio, a continuous analog voltage into a "grid" of stepped values, the lower the bit depth the more perceptible it becomes, this process is called quantization and without special measures leads to Quantization Distortion. Consider these sample values stored in 24 bit:     100, 300, 450, 550, 450, 300, 100 If this signal is converted to 16 bit, the values need reducing to fit within 16 bit (divide by 256, so maximum in 24 bit would be maximum in 16 bit), a straight rounding down (truncation) would give:     0, 1, 1, 2, 1, 1, 0 These values have big jumps, double the last, where as for 24 bit the increase was more nuanced. Anything steep or 'steppy' audio will punish, with distortion. Quantise Distortion can take the form of:     Correlated Noise: At high volumes, quantisation error sounds like white noise, at low volumes the error becomes "correlated" to the signal.     Harmonic Distortion: correlation creates harsh, gritty harmonics that sound like aggressive digital distortion rather than natural hiss.     Gating / Truncation: a signal (like a reverb tail) falls below the lowest digital step, the Least Significant Bit (LSB), it is rounded to zero. Where does the noise floor and dynamic range factor into this? whilst new values have not been created (there is no 1.5 value in fixed 16 bit), and adding values into the wave increases the noise signal (3 dB to 5 dB typically), by adding noise the perceived noise floor has been lowered and the perceived dynamic range extended. In practical terms the perceived dynamic range is extended to:     8-bit: from 48 dB to 66+ dB.     16-bit: from 96 dB to 120+ dB.     24-bit: 144 dB to 165+ dB.     32-bit: from 192 dB to 215+ dB. For 32 bit, dither noise extension would be quieter than the sound of air molecules colliding inside your ear canal, no one dithers 32 bit. 24 bit is debatable, the best Digital Audio Converters (DACs) money can buy have a signal to noise ratio of 140 dB, the extension gained is well beyond that, however for good practice many do dither 24 bit and nothing is lost doing so.

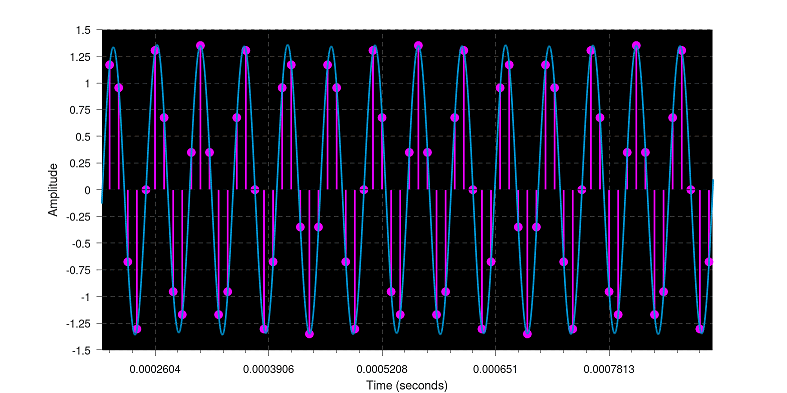
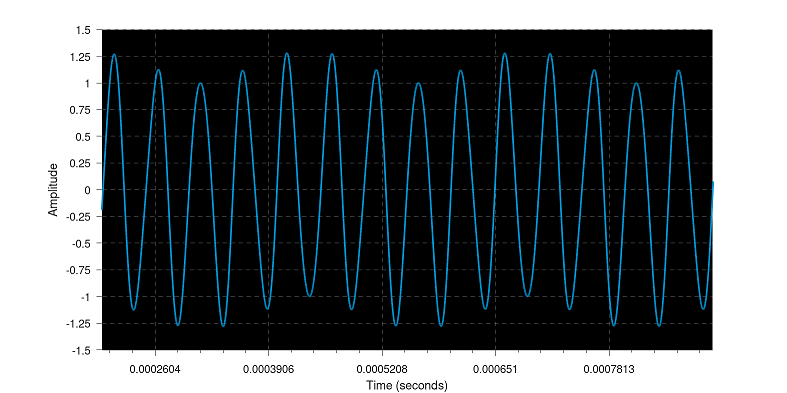
Clipping Clipping happens when audio is limited in volume, in the digital world it is when the maximum possible value which hits the hard limit of the audio bit depth. Take this sample: It was stored as 32 bit float, a high frequency wave, notice the plot on the right showing the actual sample measurements (purple dots), there are only 5 per sine, however a perfect wave form is played back from just those 5 points when converted to analog. Look at the amplitude, it extends to +1.25 and -1.25. 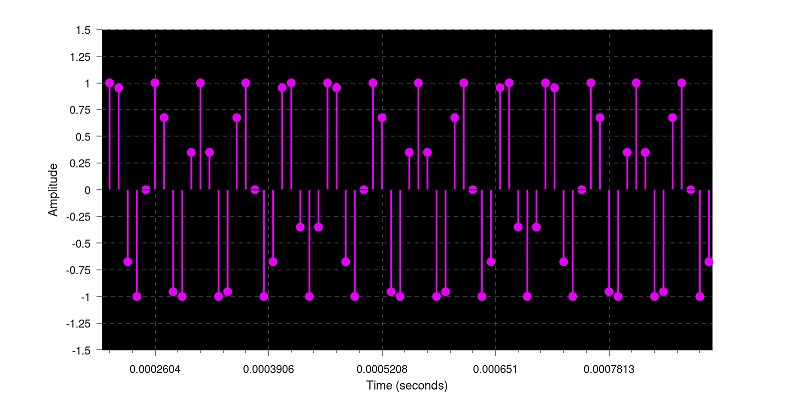If this audio is stored as 16 bit, without changing that amplitude (+1.0 is represented in 16 bit as 65535, this is the maximum value, cannot go higher), the measurements would now take the form: Nothing passes +1.0, the values are clipped, how would it actually sound? 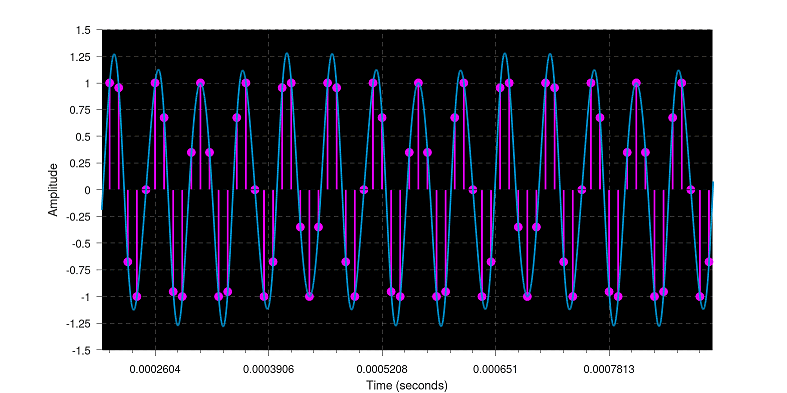The plot on the left shows the samples, the one on the right has them removed for clarity, look at the wave, it has other frequencies embedded now, distortion caused by the clipping.

Storage Considerations 16 bit uncompressed audio has 2 bytes per sample, a CD quality 3 minute track can be calculated as: 44100 (samples per second) x 3 (track length) x 60 (seconds per minute) x 2 (channels) x 2 (bytes per sample) = 31,752,000 bytes or 31 MB. 24 bit audio adds an extra byte per sample, 47 MB for the same track. At the top end is 64 bit float, each sample is 8 bytes per sample, the same track would be 127 MB, 1.5 GB for an average album! That is just for 44.1 kHz, if the sample rate was 192 kHz instead? 6.5 GB to store the album.